Hyperbolic Trisection
And the Spectrum of Regular Polygons

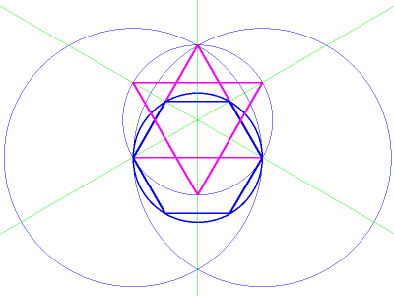
I read somewhere—back before the advent of personal computers—that it is impossible to trisect an angle with just a straightedge and a compass. Naturally I had to try it. My modus operandi was to play around with known trisections; in particular, a circle with an inscribed hexagon and a trisected diameter. The diameter in the illustration below has been trisected with a hexagram... also known as a Star of David.

image 1

Knowing that it is possible to draw a circle through any three non-collinear points, I saw the possibility of constructing two circles (one on each side of the inscribed hexagon) that would trisect the original circle and any arc whose chord coincides with the circle's diameter, as illustrated in image 2. 

image 2

In image 2, the hexagon divides the upper and lower semicircles into 3 equal parts. Segments were drawn linking the trisection points on the circle's circumference with the trisection points on the diameter. These segments have been bisected with perpendicular lines, which converge on points to the left and right. Using these points as centers, two circles have been drawn which appear to be perfectly positioned to trisect the three arcs (and their corresponding angles), which have been drawn inside the circle, to serve as examples. I see these arcs as part of a dynamic process: a single arc at three different moments in time. Imagine that the diameter is capable of expanding like a perfectly circular balloon. As it expands, its trisection points move further apart, but remain proportionally equidistant, as they follow the trisection paths marked by the two circles. At least, that was the theory.

Close, But No Cigar

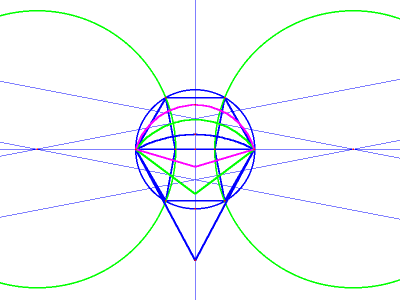
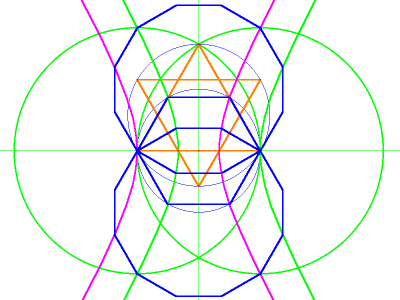
Using nothing but an unmarked straightedge and a compass, this method manages a pretty good approximation; however, on close examination, it turns out that the true trisection lines are hyperbolic, not circular. With a computer and geometry software, it is possible to find these hyperbolae. I used GEUP's “conic defined by 5 points” function. But, in order to supply the 5 points needed for this function, it is necessary to construct two more arcs with known trisection points. To do this, use the north and south poles of the original circle as the centers for two new circles and pass them through the diameter's endpoints. Then inscribe a dodecagon in each circle, as in image 3:

image 3

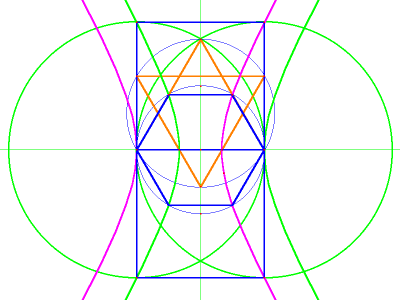
You may prefer to take the short-cut: Construct two squares (one above and one below the diameter), and use the corners of the rectangle that they form in combination:

image 4

First on one side and then on the other, using “conic defined by 5 points,” select the upper and lower corners of the rectangle, the upper and lower vertices of the hexagon, and the trisection point on the diameter. Four new curves appear. However, they represent only two hyperbolae (color-coded red and green). As if by magic, these curves vanish off the edge of the screen, and then return on the opposite sides, to intersect with the opposite endpoints of the diameter.

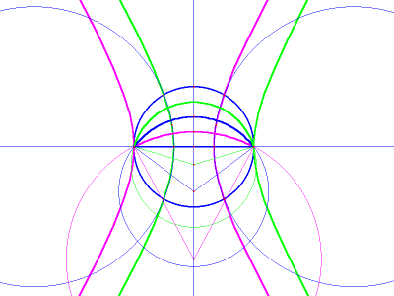
In image 5, you can see how closely the hypothetical circular trisectors approximate the true trisectors (within the boundaries of the original circle).

image 5

With this modification, the trisection works like a charm; and, as it turns out, these special hyperbolae have many other interesting properties. For example, they can be used to generate polygons with any number of sides.

The Spectrum Of Regular Polygons

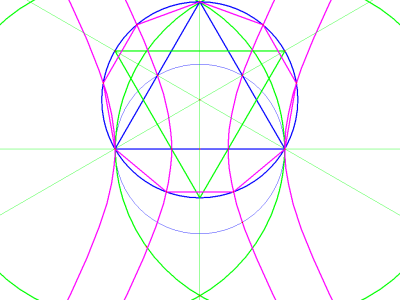
image 5a

Image 5a shows an equilateral triangle built on the diameter of our original circle. The diameter has been used as a radius to construct two larger circles centered on its endpoints. The area of overlap between these two circles is an ancient symbol known as the vesica pisces, and their intersection above the diameter is the triangle's apex. Using the triangle's center, another circle has been drawn connecting its vertices. Notice how our conic trisectors automatically mark the vertices of a nonagon on the new circle.

image 6

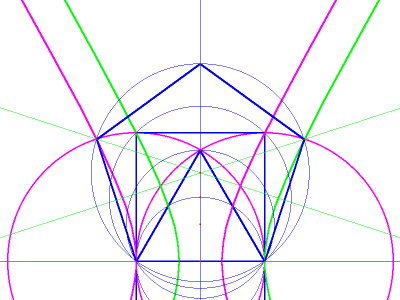
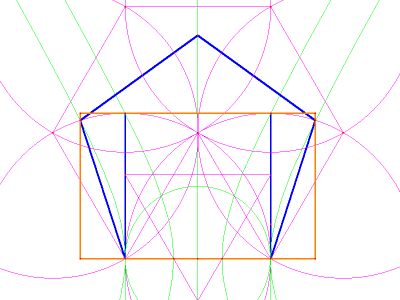
Image 6 shows how these hyperbolae can be used to construct a pentagon. The same overlapping circles that form the vesica pisces and the apex of our equilateral triangle also indicate the upper corners of a square. Follow these circles outward to the points where they intersect with the exterior pair of conic trisectors. Connect those intersection points with the diameter's endpoints, to construct the first two sides of the pentagon. The other sides can be located by using perpendicular bisectors to find the pentagon's center.

Of course, the hexagon is easy to construct. The center of the circle in which it is inscribed is located at the apex of the triangle. Likewise, you can build an octagon, a decagon, and a dodecagon by doubling the diameters of the circles in which the square, the pentagon, and the hexagon are inscribed. All of the circle's in which these polygons are inscribed should pass through the endpoints of the diameter of the original circle; and all of these polygons will have the same base, which is the diameter of the original circle.

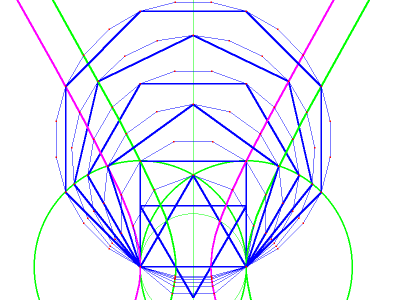
As you add to the spectrum of regular polygons, notice that our trisectors divide the arc of every side they cross into either 3 equal parts or 1/3 and 2/3. This has been made explicit in image 6a. The result is a series of polygons that increases by multiples of 3, i.e. 9, 12, 15, 18, 21, 24, etc:

image 6a

The Flower of Life

Also notable at this stage is the interesting congruency of the first four polygons (the triangle, square, pentagon, and hexagon) with the horizontal petals of the “flower of life.” The triangle points to the flower's center; the upper vertices of the square and the pentagon rest on the upper curves of its horizontal petals; and the petals themselves point to the lateral vertices of the hexagon, as you can see in image 7.

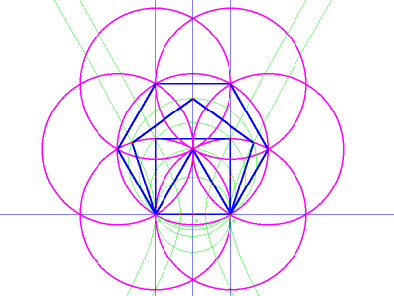
image 7

The Golden Spiral

Image 7b illustrates how these images relate to the "golden rectangle" and the "golden spiral," which visually illustrates the Fibonacci series. Two pentagons have been set side by side, so that their lateral vertices intersect. Two squares have been constructed on the same bases as the pentagons. A golden rectangle, with an inscribed golden spiral, extends from the left side of one square to the left side of the other. If this rectangle is shifted to the left, so that its left side intersects the leftmost vertice of the pentagon, it is easy to see that it is exactly the height of the square and the width of the pentagon, at the pentagon's widest point (image 7c).

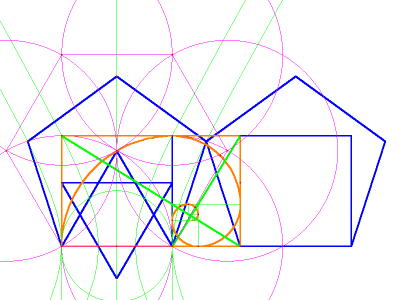
image 7b

image 7c

The Spectrum of Regular Polygons

As the construction of this spectrum progresses, a pattern emerges that should make it possible to construct the elusive 7-sided heptagon, the 11-sided hendecagon, the 13-sided tridecagon, and any other regular polygon. As mentioned earlier, all of these polygons have the same base and all of their sides are equal. As the number of sides increases, each polygon is larger than the last, and they seem to be growing outwards from the base, with the sides closest to the base describing an angular progression around two overlapping circles (colored red in the diagram below). Notice that the missing heptagon and hendecagon leave gaps in an otherwise regular progression. 

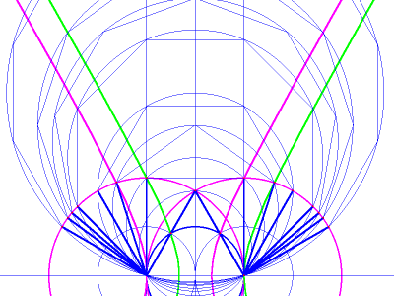
image 8

It should be possible to fill these gaps. In image 9, you can see that the other sides (like the sides immediately adjacent to the base) also describe curved pathways as they fan outward. Unlike the sides closest to the base, however, their paths are not circular.

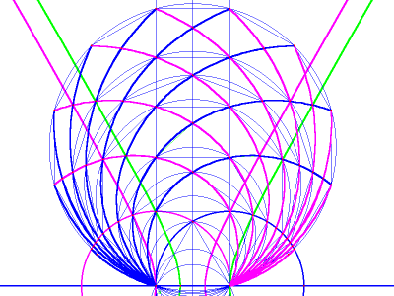
image 9

Image 9b illustrates the use of "conic by 5 points" to find the lateral vertices of the heptagon.

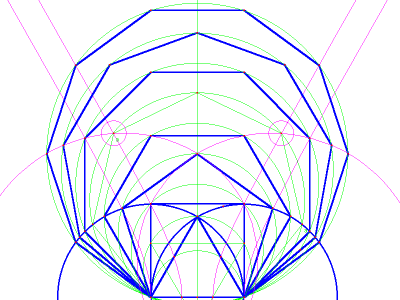
image 9b

See also:
Squaring the Circle: Sacred Geometry and
the Marriage of Heaven and Earth

Trisecting Any Angle, by Frederick R. Honey

Homepage: Song of Songs

email: webmaster@song-of-songs.net
Copyright © 2008, 2011 by Thomas Call