Squaring the Circle: 
Sacred Geometry & The Marriage of Heaven and Earth

"The mathematician's patterns, like the painter's or the poet's, must be beautiful. The ideas, like the colours or the words, must fit together in a harmonious way. Beauty is the first test: there is no permanent place in this world for ugly mathematics."

G.H. Hardy
A Mathematician's Apology

[The discoverers of the structure of DNA] Watson and Crick approached the problem through a technique chemists now use frequently... model building. They built models of the pieces of the DNA chain, and they tried various chemically reasonable ways of fitting them together. Finally, they discovered that one arrangement was "too pretty not to be true." Ulitmately, the experimental evidence of Wilkins and Franklin confirmed the "pretty structure" to be the real DNA structure."

Chemistry & Chemical Reactivity, p.392,
John C. Kotz, Paul Treichel, Paul M. Treichel, John R. Townsend

"From the domed Pantheon of ancient Rome, if not before, architects have fashioned sacred dwellings after conceptions of the universe, utilizing circle and square geometries to depict spirit and matter united. Circular domes evoke the spherical cosmos and the descent of heavenly spirit to the material plane. Squares and cubes delineate the spatial directions of our physical world and portray the lifting up of material perfection to the divine.

Constructing these basic images is elementary. The circle results when a cord is made to revolve around a post. The right angle of a square appears in a 3:4:5 triangle, easily made from a string of twelve equally spaced knots. But "squaring the circle"... drawing circles and squares of equal areas or perimeters by means of a compass or rule... has eluded geometers from early times. (2) The problem cannot be solved with absolute precision, for circles are measured by the incommensurable value pi (π = 3.1415927...), which cannot be accurately expressed in finite whole numbers by which we measure squares. (3) At the symbolic level, however, the quest to obtain circles and squares of equal measure is equivalent to seeking the union of transcendent and finite qualities, or the marriage of heaven and earth. Various pursuits draw from the properties of music, geometry, and even astronomical measures and distances. Each attempt offers new insight into the wonder of mathematical order."

Rachel Fletcher,
Squaring the Circle: Marriage of Heaven and Earth
Nexus Network Journal, Vol. 9, No. 1, 2007 119

[Squaring the circle] involves constructing an ideal square with an area equal to that of a given circle (where the radius of the circle is one, an area equal to pi) and doing so in a finite number of operations using only a straight edge and a compass. A practically identical problem is the rectification of the circle: Constructing an ideal straight line equal in length to the circumference of the circle.

Martin Gardner
Squaring the Circle

"Squaring the circle is a problem proposed by ancient geometers. It is the challenge to construct a square with the same area as a given circle by using only a finite number of steps with compass and straightedge...

In 1882, the task was proven to be impossible, as a consequence of the fact that pi (π) is a transcendental, rather than algebraic irrational number; that is, it is not the root of any polynomial with rational coefficients...

Though squaring the circle is an impossible problem using only compass and straightedge, approximations to squaring the circle can be given by constructing lengths close to π. It takes only minimal knowledge of elementary geometry to convert any given rational approximation of π into a corresponding compass-and-straightedge construction, but constructions made in this way tend to be very long-winded in comparison to the accuracy they achieve. After the exact problem was proved unsolvable, some mathematicians have applied their ingenuity to finding elegant approximations to squaring the circle, defined roughly (and informally) as constructions that are particularly simple among other imaginable constructions that give similar precision...

Among the modern approximate constructions was one by E. W. Hobson in 1913. This was a fairly accurate construction which was based on constructing the approximate value of 3.14164079..., which is accurate to 4 decimals.


Indian mathematician Srinivasa Ramanujan in 1913, C. D. Olds in 1963, Martin Gardner in 1966, and Benjamin Bold in 1982 all gave geometric constructions for

which is accurate to 6 decimal places of π.

Srinivasa Ramanujan in 1914 gave a ruler and compass construction which was equivalent to taking the approximate value for π to be

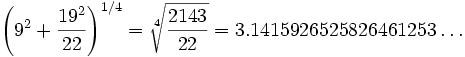
giving a remarkable 8 decimal places of π."

.

—Wikipedia: Squaring the Circle

The method described in the following article, "How to Unroll a Circle with a Straightedge and a Compass," yields a value for π that is comparable to Srinivasa's. That is to say, it is accurate to 8 decimal places, using only a straightedge and compass. Like other methods of this type, greater accurracy is possible with greater diligence; however, I am aiming for one of those "elegant" approximations mentioned in the Wikipedia article on circle squaring, cited above. Although it may take a little more time to construct, this solution is not unduly "long-winded" relative to its degree of accuracy... and it is easy to see how and why it works.

How to Unroll a Circle
with a Straightedge and a Compass

As you can see, the first few diagrams illustrate a series of circles. From the smallest to the largest, each succeeding circle has a diameter, and therefore a circumference, that is twice the length of the one before it. The third circle is inscribed with a square, and each succeeding circle is inscribed with a polygon that has twice as many sides as the one before it.

Imagine that circle C1 is able to roll around on the inner suface of circle C2. As it rolls, point C1 makes a mark wherever it touches the surface. Since the diameter and therefore the circumference of C2 are exactly twice the length of C1, point C1 marks it into exactly two parts. Likewise, if C1 rolls around on the inner surface of circle C3, which is four times the length of C1, point C1 will mark out four equal arcs.

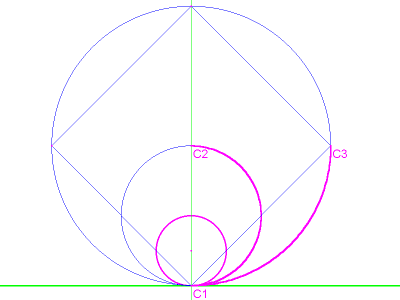image 1

Take a look at image 2. Notice the series of arcs corresponding to the first sides of the polygons. Each one is equal in length to the circumference of the smallest circle. This relationship holds true as long as the circumference of each new circle is twice the length of the previous circle, and divided into twice as many equal parts.

Each vertice on each polygon is a point marked by point C1, as it rolls around on the inner surface of the corresponding circle. Each arc corresponding to the side of a polygon is the length of the circumference of the original (unit) circle. Also notice that, if you emphasize the arcs corresponding to the first sides of these polygons, you can produce the illusion that circle C1 is unrolling into a straight line. This is an approximate solution to the problem known as the "rectification" of a circle, meaning the construction of an ideal straight line equal in length to the circumference of the circle.

Although the arc of a circle can never really be straight, it can approximate straightness with a high degree of accuracy relative to a given observer. (The obvious example is the apparent flatness of the earth.)

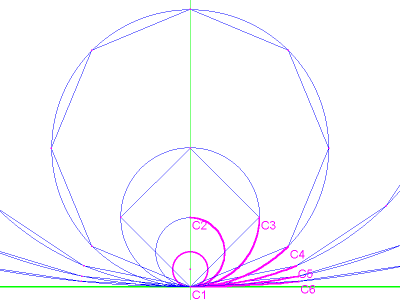image 2

No matter whether you are using geometry software or an actual straightedge and compass, a series of ever-doubling circles can be difficult to manage. Fortunately there is an easier way to construct and investigate this series of arcs.

Notice that if you construct lines that are perpendicular to the first sides of each polygon at the point where the first and second sides meet, each perpendicular line will point to the corresponding vertice on the next largest polygon.

 image 3

What this means is that you can save yourself the trouble of constructing all those circles and polygons by successively bisecting angles and reflecting them. For example, line C1-C4 can be found by bisecting angle C2-C1-C3 and reflecting the bisector around line C1-C3. The edpoint of arc C1-C4 will be the point where line C1-C4 is intersected by the perpendicular to line C1-C3. Likewise, line C1-C5 can be found by bisecting angle C3-C1-C4 and reflecting the bisector around line C1-C4. The endpoint of arc C1-C5 will be the point where line C1-C5 is intersected by the perpendicular to line C1-C4. This procedure is illustrated in image 4. (The bisectors are light green.) If you are using an actual compass, it isn't even necessary to draw a complete circle when reflecting the bisectors (as you probably know).

image 4

As the circle C1 "unrolls" in a series of arcs, their endpoints trace a curve. This is the "envelope" of the unrolling circle. If we can find this curve, or approximate it with a considerable degree of precision, then we can find the approximate point where it intersects with the baseline (the line perpendicular to the base of the unit circle), and that will give us a line nearly equal in length to the circumference (approximately rectifying a circle).

But it turns out that the curve in question is not a circle. Is it an ellipse? Some geometry applications have a function that can find a conic given 5 points (Cabri and GEUP, for example, and apparently a script can be added to Geometer’s Sketchpad). If you want to test this function, the 5 points should be clustered as closely as possible around the target. In image 5, the target is C10. Although it may be difficult to see in this image, 2 of the required 5 points were obtained by reflecting C8 and C9 to the other side of the baseline. Notice that the resulting ellipse is less and less accurate as it moves away from the target, so that it misses the end of arc C2 by a wide margin. Nevertheless, this technique yields a value for π that is accurate to 12 decimal places.

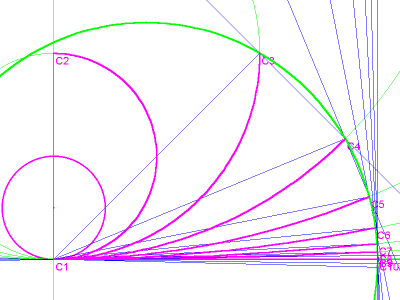image 5

Of course I've broken the rules in this example by using a computer to construct an ellipse. In a moment, however, we will take a look at a method that yields a value for π that is accurate to 8 decimal places, using only a straightedge and a compass. But first, let's stop and ask ourselves what exactly we're going to do with our "linear approximator," once we manage to find it. We will then have to use it somehow to construct a square with an area that is equal to the area of our original circle. It isn’t simply a matter of dividing the line into four parts and folding it into a square. (All that would get us is a square with a perimeter nearly equal to the circumference.) So, given a line that is nearly equal to the circumference, here are three ways to almost do the impossible:

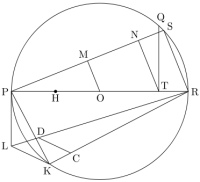
The first is given by Alexander Bogomolny, on his Cut the Knot website. Image 6 illustrates his method for finding the square, together with my own method for finding the linear approximator. According to mister Bogomolny:

"Thus it's impossible to square a circle using a straightedge and a compass; but like the problem of angle trisection, this one can be solved by other means. Have a look at the diagram on the right. Assume a circle of unit radius is rolled half a turn on a straight line. Then the distance between the points A and B will be exactly π. If we draw a semicircle on AC = AB+1 as a diameter, and continue the vertical radius of the right circle to the intersection with the semicircle at a point D, then AB×BC = BD2. Which, of course, solves the famous problem because AB = π and BC = 1."

A. Bogomolny,
Squaring the Circle,
from Interactive Mathematics Miscellany and Puzzles
http://www.cut-the-knot.org/impossible/sq_circle.shtml,
Accessed 09 September 2007

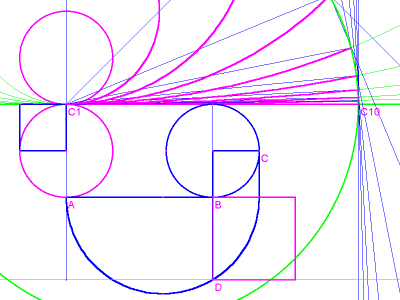image 6

In order to convert this generalized algebraic solution into a precise geometric solution, all we need is a distance equal to 1/2 the circumference laid out on a straight line. So I've reflected the unit circle around the baseline and divided the distance C1-C10 in half.

This next method I found on the Slice of Pi website (Squaring a Rectangle). Once again the unit circle has been reflected around the baseline. Use the linear approximation of the circuference (C1-C10), and the diameter of the unit circle to construct a rectangle. (A-C1-C10-B in image 7) The area of this rectangle is very close to 4 times the area of the unit circle.

image 7

Obviously if we divide that area into 4 equal parts, we have a rectangle that is almost equal to the area of the unit circle.

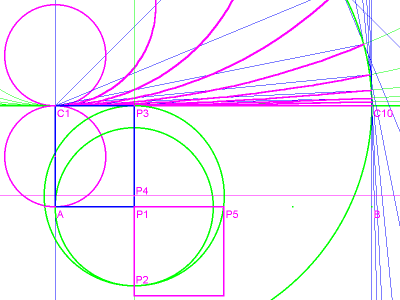image 8

In this case, in order to square the circle, we first need to square a rectangle. The length of this rectangle is equal to the diameter of the unit circle, and its width is 1/4 the approximate circumference. First use the width of the rectangle as the radius of a circle (A-P1 in image 8, with the center P1). Bisect the distance P2-P3 to find the center of a second circle, P4, and draw circle P4. Extend the radius A-P1 to intersection P5 on circle P4, and use the distance P1-P5 to construct a square. That's the square we're looking for!

Here is an even easier way to find it... the last method to come to my attention:

Once again, the unit circle has been reflected around the baseline, and the diameter of the reflected circle forms the width of a rectangle that extends from C1 to C10. Once again, this rectangle has been divided into four equal parts, and each part has an area that is very close to that of the unit circle. In this case, however, our rectangle has been divided so that the widths of the smaller rectangles equal the radius of the unit circle. A semicircle with the diameter A-C has been drawn on one side of rectangle A-C-D-C1. A-C intersects with the unit circle at point B. A line perpendicular to A-C has been drawn from B to the point where it intersects with the semicircle (point E). The line A-E is the first side of our (almost) squared circle.

Now let's put it all together and find this square using only a straightedge and compass. Use the bisection/reflection technique described earlier, and, starting with the bisection of angle C2-C1-C3, carry it out to point C9. That's only 6 bisections.

Do NOT bisect the last ANGLE (which in this example is C8-C1-C9). Instead, draw a line connecting the last 2 points in the series (C8 and C9), and divide that line into two equal parts with a perpendicular bisector.

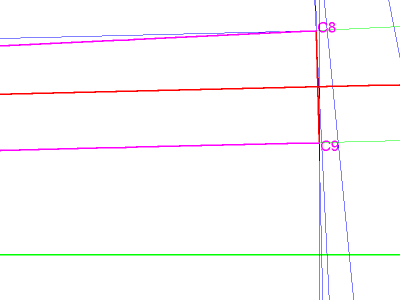image 9

That bisector will fall short of center C1, and intersect with the baseline at point Z. Let Z be the center of a new circle with radius Z-C9. 

image 10

Find the point where that circle intersects the baseline and label it C10. That's the point we've been looking for.

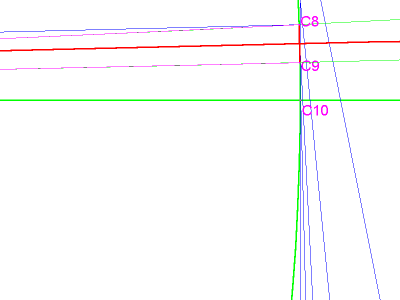image 11

In this final step, I've used GEUP geometry software to compare the circumference of the unit circle with the "linear approximation."  In this example, when the distance from C1 to C10 is divided by the circumference, the difference is found to be 1.000000001. The difference between the area of the circle and the area of the square is likewise found to be 1.000000001.  Dividing the linear approximation by the diameter of the unit circle yeilds the value 3.1415926578, which is pi (π), accurate to 8 decimal places.

image 12

Despite its ever increasing accuracy, this process of doubling polygons, or bisecting and reflecting their first sides, will never result in a straight line that is exactly equal to the circumference of the original circle. The "unrolling" arcs get flatter and flatter, like their corresponding chords, but never quite merge and "become one" with them. Once a circle, always a circle, no matter how infinitely large it becomes. Likewise the corresponding array of perpendiculars never quite settles on the point that is pi (π) times the diameter from the base of the unit circle. This is not because the circumference doesn't have a definite length, but because our measuring rod does not have a definite length. Our measuring device is a ratio of circumference and diameter... a never ending number. Thus, if the microcosm is infinitely deep, the process of measurement can go on forever. Nevertheless, after 6 angular bisections and a perpendicular bisection, we already have a result that is easily plumb enough to build a house by. (Bear in mind that the accuracy is greatly increased by using an ellipse [geometry software, conic given 5 points] or a circle [using a compass] to project the envelope of the unrolling circle onto the baseline.)

What we have here is a perfect illustration of Zeno's paradox concerning the race between Achilles and the tortoise. But in this case the tortoise's victory is not merely rhetorical. How does he manage to elude swift Achilles? He jumps down a rabbit hole into wonderland and leaves the guy forever reducing the distance between them by half, as they disappear into the (theoretically) infinite smallness of the microcosm. 

Zeno's Paradox: Achilles and the Tortoise

"Zeno's paradoxes are a set of problems devised by Zeno of Elea to support Parmenides' doctrine that "all is one" and that, contrary to the evidence of our senses, the belief in plurality and change is mistaken, and in particular that motion is nothing but an illusion.

Achilles and the tortoise: "You can never catch up."

“In a race, the quickest runner can never overtake the slowest, since the pursuer must first reach the point whence the pursued started, so that the slower must always hold a lead."

—Aristotle, Physics VI:9, 239b15

In the paradox of Achilles and the Tortoise, we imagine the Greek hero Achilles in a footrace with the plodding reptile. Because he is such a fast runner, Achilles graciously allows the tortoise a head start of a hundred feet. If we suppose that each racer starts running at some constant speed (one very fast and one very slow), then after some finite time, Achilles will have run a hundred feet, bringing him to the tortoise's starting point; during this time, the tortoise has "run" a (much shorter) distance, say one foot. It will then take Achilles some further period of time to run that distance, in which said period the tortoise will advance farther; and then another period of time to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles reaches somewhere the tortoise has been, he still has farther to go. Therefore, Zeno says, swift Achilles can never overtake the tortoise. Thus, while common sense and common experience would hold that one runner can catch another, according to the above argument, he cannot; this is the paradox. 

----Wikipedia: Zeno's Paradoxes

Filling In The Gaps

image 13
Rectification of a Circle

As illustrated in image 13, the series of arcs produced by doubling polygons, or bisecting and reflecting their first sides, is rather sparsely populated. The virtue of this technique is that it rapidly converges on a linear approximation of the circumference. Yet, it would be interesting to have more information about the overall curve, or "envelope," formed by the endpoints of the "unrolling circle." Is it possible to fill in the gaps and create a more detailed array? And would this provide us with a more accurate linear approximation? 

Image 14 illustrates a hexagram or Star of David inscribed in circle C. Smaller circles have been drawn around the star's six triangles. A seventh circle fits neatly between them, in the center. All seven circles have the same diameter and area.

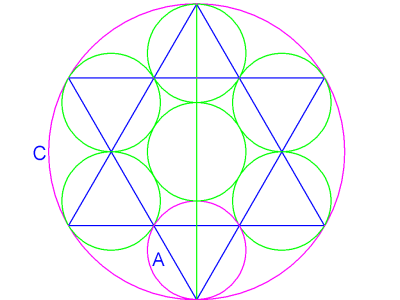image14

The circle at the bottom has been labled A. The diameter of A is 1/3 that of C, and its area is 1/9th... which is to say that the negative space between the seven circles in C equals the area of two more circles, for a total of nine. 

Circle B, in image 15, has a diameter which is twice that of the unit circle A... one less than circle C. The upward pointing "male" half of the hexagram or Star of David has been de-emphasized, in this figure, and an arc has been drawn on circle C enclosing two of the "female" triangle's three sides. The length of this arc is exactly equal to the circumference of circle B.

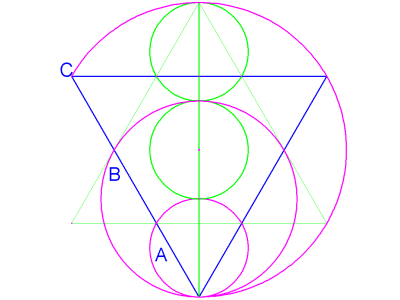image 15

Using the same unit of measure (the diameter of A) we can build a spectrum of regular polygons, and produce a series of arcs that are all equal to the circumference of circle B. Thus the downward, "female" triangle becomes the first polygon in a series ranging from 3 to any number of sides (3 through 10, in image 16). Each succeeding polygon is inscribed in a circle with a diameter that is 1 unit lager than the last. And each succeeding polygon has one additional side. The arcs are drawn so as to span the first and second sides of each polygon. Although A is the smallest circle in the series, B is regarded as the first because the length of its circumference is the basis of the series, and every arc in the array is equal to it.

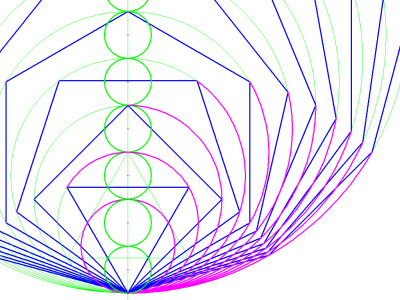image 16

Image 17 adds the element of symmetry to this construction. Instead of spanning the first and second sides, and "unrolling" to the right, the arcs in this figure span the first sides only... on the right and left. The resulting series of arcs seems to part at the top and open outward like a budding flower. In this case, the combined length of each symmetrical pair exactly equals the circumference of circle B, the first circle in the series.

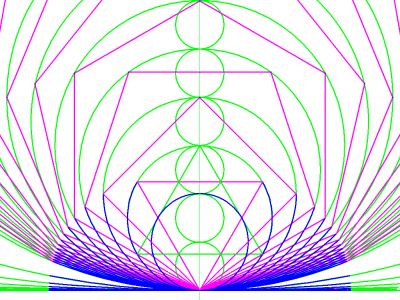image 17

For an even more detailed array of arcs, unit A can be divided in half, and additional polygons interpolated. This entails "recalibrating" the existing polygons by doubling the number of sides. Thus, when the triangle is replaced with a hexagon and the square is replaced with an octagon, it is possible to insert a heptagon between them. Figures 18 and 19 show the result of this procedure applied to the first few polygons. Notice that the "unrolling" arcs now encompass four sides instead of two. This construction rapidly becomes so densely populated that it is difficult to proceed without some sort of algorithmic automation. Hence, the "envelope" of the "unrolling" circle (in image 19) was found by combining this technique with the original technique of bisection and reflection.

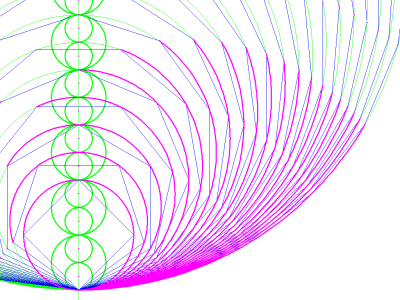image 18

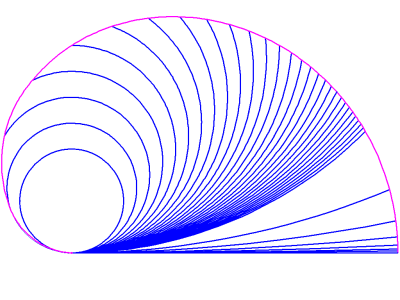image 19 

Rectification of a Circle

Image 20 illustrates the "recalibration" of the symmetrical array shown in image 17.

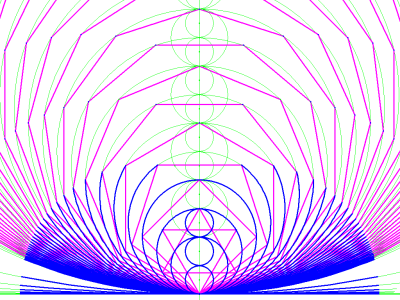image 20

Sacred Geometry and
The Marriage of Heaven and Earth

"At the symbolic level... the quest to obtain circles and squares of equal measure is equivalent to seeking the union of transcendent and finite qualities... or the marriage of heaven and earth."

Rachel Fletcher,
Squaring the Circle: Marriage of Heaven and Earth
Nexus Network Journal, Vol. 9, No. 1, 2007 119

"Squaring the circle" can represent the union of eternal and finite qualities, symbolizing the fusion of matter and spirit, metaphorically described as a marriage of heaven and earth. Interestingly, the hexagram (Star of David)---which is the key to filling in the gaps of the "unrolling" circle---has the same symbolic meaning:

"The hexagram is a Mandala symbol called satkona yantra or sadkona yantra found on ancient South Indian Hindu temples built thousands of years ago. It symbolizes the Nara-Narayana, or perfect meditative state of balance achieved between Man and God, and if maintained, results in "Moksha," or "Nirvana" (release from the bounds of the earthly world and its material trappings)." 

"Within Indic lore, the shape is generally understood to consist of two triangles--one pointed up and the other down--locked in harmonious embrace. The two components are called 'Om' and the 'Hrim' in Sanskrit, and symbolize man's position between earth and sky. The downward triangle symbolizes Shakti, the sacred embodiment of femininity, and the upward triangle symbolizes Shiva, or Agni Tattva, representing the focused aspects of masculinity. The mystical union of the two triangles represents Creation, occurring through the divine union of male and female."

In alchemy, the two triangles represent the reconciliation of the opposites of fire and water. Non-Jewish Kabbalah (also called Christian or Hermetic Kabbalah) interprets the hexagram to mean the divine union of male and female energy, where the male is represented by the upper triangle (referred to as the "blade") and the female by the lower one (referred to as the "chalice").

—Wikipedia: Hexagram

This symbolic meaning, conveyed by both "squaring the circle" and the hexagramic Star of David, is the real focus of this website... referred to throughout as the marriage or wedding of heaven and earth. 

One of the hexagram's triangles points up and outward to the heavens and the macrocosm; the other points down to Earth and inward to the microcosm. The downward triangle has long been regarded as female because of its resemblance to the delta of venus *, and because it is through woman that we enter into this supposedly "lower," "material" existence on Earth, under the heavens. Woman is stereotypically associated with birth... the giving of life... and man is stereotypically associated with war, death, and gnostic liberation of spirit from its material entanglement; hence, the symbolism of chalice and blade. Also... stereotypically... man is the explorer who ranges far and wide, while woman prefers the comfort of hearth and home (even though we all live with the tension of these extroverted/introverted, expansive/contractive impulses). The hexagramic Star of David represents these forces, in harmonic balance. On a physiological level, it represents homeostasis: a dynamic balance of the biological processes of creation and destruction (anabolism and catabolism). And as the Sanskrit 'Om' and the 'Hrim' it can also signify the biosphere... "man's position between earth and sky"... where we "live, breathe, and have our being." 

Psychologically and spiritually, the hexagram symbolizes the enlightened interpenetration of the essential Self---the Source of the universe, the "Ground of Being"---and the socially constructed egocentric personality. Thus the marriage of heaven and earth, in its most potent form, is the experience at the heart of the "perennial philosophy," variously known as mystical union, kensho, satori, enlightenment, or unitive consciousness. For myself, this marriage signifies the evolutionary process by which this deeper mode of consciousness might eventually become the norm... in effect, the unfolding and establishment of an earthly paradise. 

The "release from the bounds of the earthly world and its material trappings" known as moksha or nirvana is simply... and in more empirical terms... the marriage of subject and object---the psychological dissolution of the boundaries between self and other (tat tvam asi, thou art that).* This has often been misunderstood as liberation of the soul from the degraded, corruptible, physical body; but surely the actual, authentic experience entails a dissolution of all such dualisms separating oneself from the world.

...it is likely that our parents found us in our cribs long before we found ourselves there, and that we were merely led by their gaze, and their pointing fingers, to coalesce around an implied center of cognition that does not, in fact, exist. Thereafter, every maternal caress, every satisfation of hunger or thirst, as well as the diverse forms of approval and rebuke that came in reply to the actions of our embodied minds, seemed to confirm a self-sense that we, by example, finally learned to call "I"--- and thus we became the narrow locus around which all things and events, pleasant and unpleasant, continue to swirl.

The sense of self seems to be the product of the brain's representing its own acts of representation: its seeing of the world begets an image of a one who sees. It is important to realize that this feeling---the sense that each of us has of appropriating, rather than merely being, a sphere of experience---is not a necessary feature of consciousness. It is, after all, conceivable that a creature could form a representation of the world without forming a representation of itself in the world. And, indeed, many spiritual practitioners claim to experince the world in just this way, perfectly shorn of self...

As a mental phenomenon, loss of self is not as rare as our scholarly neglect of it suggests. This experience is characterized by a sudden loss of subject/object perception: the continuum of experience remains, but one no longer feels that there is a knower standing apart from the known. Thoughts may arise, but the feeling that one is the thinker of these thoughts has vanished. Something has definitely changed at the level of one's moment-to-moment experience... the disappearance of anything to which the pronoun "I" can be faithfully attached...

---Sam Harris, "The End Of Faith,"
© 2004, p. 212-213

One of the most highly regarded modern exemplars of this vista of consciousness was the Indian sage, Ramana Maharshi. In his forward to the book, "Talks with Ramana Maharshi," contemporary philosopher, Ken Wilber, remarked:

I am often asked, "If you were stranded on a desert island and had only one book, what would it be?" The book you are now holding in your hands---Talks with Ramana Maharshi---is one of the two or three I always mention. And 'Talks' tops the list in this regard: it is the living voice of the greatest sage of the twentieth century and , arguably, the greatest spiritual realization of this or any time.

Regarding dissolution of the false dichotomy between "I and thou," Ramana made the following observation:

From where does this "I" arise? Seek for it within; it then vanishes. This is the pursuit of wisdom. When the mind unceasingly investigates its own nature, it transpires that there is no such thing as a mind. Get rid of the "I" thought. When "I" ceases to exist, there is no grief and there is peace."

---Ramana Maharshi

Or, in the language of modern science:

Man as an organism is to the world outside like a whirlpool is to a river: man and world are a single natural process, but we are behaving as if we were invaders and plunderers in foreign territory. For when the individual is defined and felt as the separate personality or ego, he remains unaware that his actual body is a dancing pattern of energy that simply does not happen by itself. It happens only in concert with myriads of other patterns---called animals, plants, insects, bacteria, minerals, liquids, and gases. The definition of a person and the normal feeling of "I" do not effectively include these relationships. You say, "I came into this world." You didn't; you came out of it, as a branch from a tree."

---Alan Watts,
Does It Matter © 1968, 1969, 1970, p.23

An engaging contemporary account of this unitive experience is given by Trisha Feuerstein, in her husband's book Sacred Sexuality. This is what she wrote:

"My first memory of that incident is of awakening one morning after a night of lovemaking and feeling as if I had not been asleep. I felt as though I was conscious or constantly awake on some higher plane. That entire day I remember feeling totally and perfectly relaxed.

In this perfect relaxation I stood outside of time. It was as if time normally flowed in a horizontal plane, and I had somehow stepped out of this horizontal flow into a timeless state. There was absolutely no sense of the passage of time. To say there was no beginning or ending of time would seem irrelevant. There was simply no time.

I remember coming home from work a few days later, standing in the living room of my little studio apartment, and suddenly realizing that I had no edges. There was no me. The thought arose, and these are the exact words, "This is what I AM in truth." I remember looking over to the door of my apartment and thinking, "There is no difference between door jambs and smog." There is no difference between anything whatsoever. Everything is the same. There is only apparent difference.

I remember that the thoughts also arose, "You could shoot me in this moment and I would laugh." Everything material seemed superfluous. It was all spontaneously and playfully arising from one great source, and it could just as well cease to arise in any moment.

Somehow I had become infinity with eyes. I felt as if I had just been born in that moment, or that I had been asleep all my life and had just awakened. I also remember thinking that this was the true condition of everyone and that everyone could know this.

This particular moment remains, seventeen years later, the single most significant moment of my life. It was also the most ordinary, simple, happy, normal, neurosis-free moment of my life. I was simply being what I AM, and what everyone else IS, in truth.

I remained in this state of edgelessness for about three weeks, and life was intensely magnified. When I walked, I felt so light it was as if my feet did not touch the ground. I had no appetite for food---in fact, most of what I tried to eat left a strange metallic taste in my mouth. And although I ate almost nothing during this period, I lost no weight. I remember telling my lover that it felt as if my spine were plugged into the "universal socket" and that it was a source of infinite energy.

During this time I was more creative than I had ever been---or have been since---both at work and outside of work. All the limits on my thinking were no longer in place. I also became prescient---seeing into the future and then later experiencing the scenes I had foreseen down to the last detail. This astonished me.

I also remember sitting at my desk at work one day and turning to look at one of my officemates. In an instant I was drowning in bliss, overwhelmed with love and compassion for my fellow worker, and for every being and thing I looked at. I loved everyone, including my lover, the same---infinitely. There was really no one separate to love. Tears silently rolled down my cheeks. I felt infinite love and infinite pain at the same time, the pain arising from realizing the power and primacy of love, yet how little we love.

I remember thinking that this universal love is what the Madonna symbolizes. Then suddenly I felt as if I were the source of all creation, that the universe was arising from me, or through me---from whatever this infinite thing was I had become."

---Trisha Feuerstein
"Sacred Sexuality," by Georg Feuerstein

More on this at Song of Songs.net.

See also: Hyperbolic Trisection and the Spectrum of Regular Polygons
Home Page: Song of Songs.net

email: webmaster@song-of-songs.net
Copyright © 2007 - 2011, by Thomas Call.