Hyperbolic Trisection
And the Spectrum of Regular Polygons

 Continued from page one.

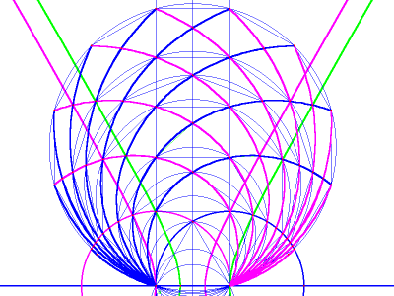
Fig. 9

If you begin a new construction, using GEUP's "construct a regular polygon" function, and start with a heptagon; and if you use the method described in this article to construct a pair of conic trisectors on its base, you will see that they intersect precisely with the heptagon's lateral vertices. But is it possible to find these vertices and construct a heptagon without resorting to GEUP's automatic polygon function? A second line or curve is needed to precisely locate these vertices on an x/y axis. To this end, GEUP's "conic defined by 5 points" has been used in figure 9b to find the trajectory of the vertices that are two steps away from the spectrum's base. Two of the heptagon's vertices should be marked by the points where that trajectory intersects with our conic trisectors. However, there is a tiny error when GEUP tries to calculate this trajectory. I think this is a problem with GEUP's algorithm, rather than a disproof of the hypothesis that the heptagon's vertices lie along the same curves that join, or are described by, the vertices of so many other regular polygons.

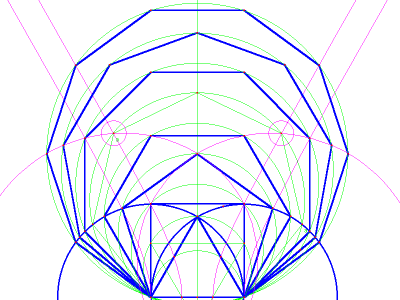
Fig. 9b

In Figure 10 I've tried to reduce the amount of error, by using a different curve. Notice that the circle with the inscribed triangle intersects two sides of the square (one on the left, and one on the right). Likewise, the circle with the square intersects two sides of the pentagon, and the circle with the pentagon intersects two sides of the hexagon. Obviously this pattern suggests that the circle with the hexagon will intersect with the sides of the heptagon. All we have to do to find the unknown intersection is find the trajectory of the known intersections, using either the “conic defined by 5 points,” or the “arc given 3 points” function. 

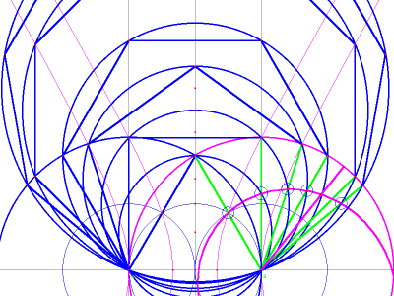
Fig. 10

Notice that it is necessary to construct an octagon and a nonagon, so that there will be known intersections on both sides of the missing heptagon. Both of these are easy to build. As mentioned earlier, our conic trisectors automatically mark the vertices of a nonagon on the circle around the triangle. See Figure 11, and notice that the two sides adjacent to the base of the nonagon can be extended to form the sides of a larger nonagon, with the same base as the rest of the spectrum.

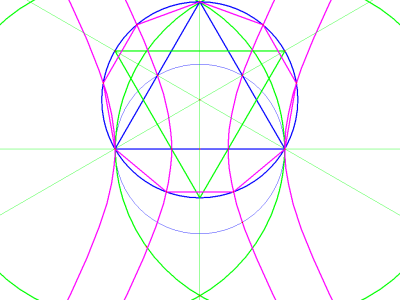
Fig. 11

When the octagon and the nonagon are in place, use “conic by 5 points” to generate a curve that intersects with the circle containing the hexagon. Draw a line through that intersection with one endpoint on the base and one endpoint on the same circle where all the other first sides terminate. Revisit figure 10, for an illustration of this proceedure. The completed heptagon is shown in figure 12. Notice that the two inner hyperbolae pass through the heptagon's upper vertices, on the right and left sides.

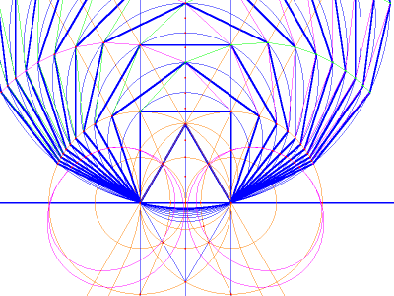
Fig. 12

Figure 12 shows how the methods in this article have been used to construct polygons with 3 to 14 sides. GEUP's “conic defined by 5 points” and “arc given 3 points” both seem to work for this purpose. However, GEUP sometimes produces inconsistent results when measuring small differences. The margin of error can be as much as + or – .01 cm.  At high magnifications, points and lines sometimes move erratically and disappear. Because of this resolution problem, it is not clear to me whether the arc function is as accurate as the conic function. Also bear in mind that neither of these functions can produce curves with angles that are constantly changing. Yet the curves for finding unknown sides, in this method, cannot be fully defined with only 3 or 5 points. As a result, if you are using GEUP, or other software with similar limitations, the points chosen for these functions should be set as closely as possible around the unknown side. And as new polygons are added, it will be necessary to use the new intersections that they provide, in order to fill in the new gaps (instead of trying to use only one arc or one ellipse for all). Notice, in figure 12, that there are two red ellipses on the right, and two on the left, that coincide with each other on their upper sides. Using “conic defined by 5 points,” two overlapping sets of 5 points were chosen, forming an “envelope” of ellipses, in order to construct polygons with a range of 3 to 14 sides.

In figures 10 and 12, I used “conic by 5 points” because it seems to be more accurate, and my main concern was to take accurate measurements, to see if the method really works. However, In figure 13, the “arc given 3 points” function was used, for the sake of clarity, to emphasize the curves described by the vertices. Unlike the conic function, the arc function doesn't project beyond the points that are assigned to it, which in this case would create a tangle of unecessary lines.

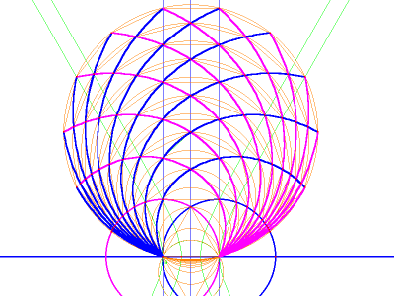
Fig. 13

By building two additional polygons with 24 and 48 sides, and by reflecting the entire structure to the area below the base line, it is possible to approximate the trajectories of these curves, and to determine their destinations, as in figure 14:

Fig. 14

One last observation: Other sets of polygons are implied by this construction. If you connect the upper corners of the sides adjacent to the base with the opposite endpoints on the diameter, you can create a series of regular polygons whose upper sides all share the same endpoints—like a series of roofs with different pitches—all resting on the diameter of the original circle, as in figure 15. 

Fig. 15

These same lines—forming the upper sides in this series—also intersect with the interior trisectors at points that can be used to find the bases of yet another series. In this series (shown below), the polygons are all pointing downward, and their bases follow the paths laid out by the interior pair of conic trisectors.

Fig. 16

See also:
Squaring the Circle: Sacred Geometry and
the Marriage of Heaven and Earth

Homepage: Song of Songs

email: webmaster@song-of-songs.net
Copyright © 2007 by Thomas Call